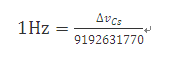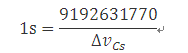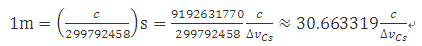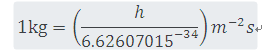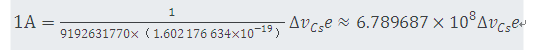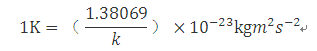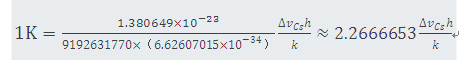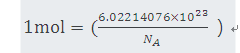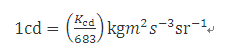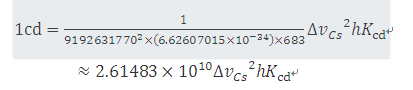SI基本单位在量子化演进中是如何定义的
浏览数:8039 发表时间:2019-03-01
国际单位制(以下简称SI)自建立以来最新最重要的一次修订已在2018年第26届国际计量大会上产生,并记录在SI手册(第9版)。在2018年的定义之前,SI是通过7个基本单位及由基本单位的幂次、乘积构成的导出单位定义的,而通过7个确定常数的固定数值给SI下定义更加有影响。其差别是原则上不需要之前的定义,因为所有单位、基本单位和导出单位都可以直接由确定常数构成。尽管如此,基本单位和导出单位的概念是保留的,不仅因为它有用,在历史上获得公认,也因为它对保持ISO/IEC 80000系列国际标准规定的国际量制(ISQ) 是必要的,该标准指定的基本量和导出量需与SI基本单位和导出单位相符合。SI基本单位如表1所示。
表1 SI基本单位
基本量 | 基本单位 | ||
名称 | 典型符号 | 名称 | 符号 |
时间 | t | 秒 | s |
长度 | l, x, r, etc | 米 | m |
质量 | m | 千克 | kg |
电流 | I, i | 安培 | A |
热力学温度 | T | 开尔文 | K |
物质的量 | n | 摩尔 | mol |
发光强度 | Iv | 坎德拉 | cd |
从依据确定常数的固定数值定义SI出发,通过适当使用这些确定常数中的一个或多个给出下列定义集,推导出7个基本单位的每一个定义。
一、 秒(The second),符号s,是时间的SI单位
它由铯频率ΔνCs的固定值定义,即:使得铯-133原子基态两个超精细能级之间跃迁频率达到9192631770Hz,Hz等于。
这个定义准确地表明:ΔνCs= 9 192 631 770Hz,反向推导,根据确定常数ΔνCs值即可给出单位秒的一个表达式:
或者
这个定义的结果是秒等于未受干扰条件下铯-133(133Cs)原子在稳定基态两个超精细能级之间跃迁9 192 631 770个辐射周期持续的时间。
提及未受干扰的原子是为了说清楚SI秒的定义是基于一个独立的、不受任何外部场(如环境黑体辐射) 干扰的铯原子。
如此定义的秒是广义相对论中本征时间的单位。为了提供一个协调的时间标尺,不同地点不同基准钟的信号被结合在一起,以便做相对铯频率变化的修正。
国际计量委员会(CIPM)基于挑选出来的原子、离子或分子的光谱线数量,已采用了多种秒的次级复现形式。只是其中一部分复现具有较高的稳定性,能够确定这些谱线无扰动频率和不低于基于铯-133超精细跃迁复现的秒的相对不确定度。
二、 米(The metre),符号m,是长度的SI单位
它采用光在真空中速度c的固定数值299 792 458定义,单位为ms-1,其中秒依据铯频率ΔνCs定义。
这个定义准确地表明:c = 299 792 458ms-1,反向推导,根据确定常数c和ΔνCs即可给出米的准确表达式:
这个定义结果是1米等于光在真空中行进1/299 792 458秒时间的路径长度。
三、千克(The kilogram),符号kg,是质量的SI单位
它采用普朗克常数h的固定数值6.626 070 15×10-34定义,其单位为J s,等于kg m2s-1,其中米和秒是依据c和ΔνCs定义。
这个定义准确地表明:h= 6.626 07015 ×10-34kg m2s-1,反向推导,根据规定常数h、ΔνCs和c即可给出千克的准确表达式:
或者
这个定义的影响是朝向定义单位kg m2s−1 (运动量、角动量两个物理单位)。这导致了质量单位的定义,用普朗克常数h连同秒和米的定义一起表示。
以前的千克定义由国际千克原器的质量值m(K)确定,m(K)精确地等于1千克,普朗克常数h的值必须通过实验来确定。现在的定义精确地确定了h的值,而原器的质量现在必须通过实验来确定。
该定义中的普朗克常数的数值是这样确定的:在它被选用的时候,千克等于国际千克原器质量,m(K) = 1 kg,其相对标准不确定度为2×10- 8,这是当时对普朗克常数值的综合最优估计的标准不确定度。
还请注意,根据目前的定义,原则上原级复现能在质量标尺的任何一点建立。
四、安培(The ampere),符号A,是电流的SI单位
它由元电荷e 的固定数值1.602 176 634×10-19定义,其单位为C,等于A s,其中秒是ΔνCs依据定义。
这个定义准确地表明:e = 1.602 176 634 ×10-19As,反向推导,根据确定常数e和ΔνCs即可给出单位安培的准确表达式:
或者
这个定义的结果是1安培等于1/(1.602 176 634×10−19)个元电荷每秒流动所形成的电流。
以前,安培的定义基于真空磁导率(也称为磁性常数)μ0值恰好是4π×10-7Hm-1= 4π×10-7NA-2的载流导线之间的力,其中H、N分别表示互相关联的导出单位亨利和牛顿。安培的新定义用固定值![]() 代替μ0,而且μ0结果必须用实验方法确定。
代替μ0,而且μ0结果必须用实验方法确定。
同时,由于真空介电常数(也称为电常数)ε0,真空的特性阻抗Z0,真空的导纳Y0分别等于1/μ0c2、μ0c和1/μ0c,ε0、Z0、Y0的值现在也须各自用实验方法确定,而且受和μ0一样的相对标准不确定度影响,因为c是已知精确的,乘积ε0μ0= 1/c2和商Z0/μ0=c保持精确值。在采用现在安培定义的时候,μ0=4π×10-7H/m,具有2.3×10−10的相对标准不确定度。
五、开尔文(The kelvin),符号K,是热力学温度的SI单位
它由玻尔兹曼常数k的固定数值1.380 649×10-23 J K-1定义,其单位J K-1等于kg m2s-2K-1,其中千克、米和秒是依据h、c和ΔνCs定义。
这个定义准确地表明:k= 1.380 649×10-23kg m2s-2K-1,反向推导,根据确定常数k 、h和ΔνCs即可给出开尔文的准确表达式:
或者
这个定义的结果是1 K等于热能kT发生1.380 649×10−23J的改变导致的热力学温度变化量。
以前的开尔文定义是基于一个被分配给水的三相点温度TTPW的精确数值,即273.16 K。由于现在开尔文的定义确定了k的数值,而不是TTPW,所以后者必须通过实验来确定。在采用现在定义的时候,TTPW等于273.16K,相对标准不确定度3.7×10-7,这是基于重新定义之前对k的测量。
由于过去用温度标度来定义,通常的做法是用与接近冰点的参考温度T0= 273.15K差来表示热力学温度,符号T。这种差被称为摄氏温度,符号t,由如下量方程定义:
t=T-T0
摄氏温度的单位为摄氏度,符号为℃,按照定义其量级与单位开尔文相等。一个温度差或区间可以用开尔文或摄氏度表达,不论何种情况,温度差的数值都是一样的。正是由于这个关系,用摄氏度表达摄氏温度的数值与用开尔文表达热力学温度的数值有关。
t/℃=T/K-273.15
开尔文和摄氏度也是1989年国际计量委员会CIPM的建议5 (CI-1989, PV, 57, 115)中采用的1990年国际温标(ITS-90)的单位。注意ITS-90定义了两个量T90和t90,与热力学温度T和t相配。
同样注意,目前开尔文定义的原级复现原则上可以在温标内任何一点上建立。
六、摩尔(The mole),符号mol,是物质的量的SI单位
一摩尔恰好包含6.022 140 76×1023个基本粒子。当用单位mol-1表达时,这个数是阿伏伽德罗常数的固定数值NA,也称阿伏伽德罗数值。
物质的量,符号n,是对指定基本粒子数目测量的一个量制。基本粒子可以是原子、分子、离子、电子及其他粒子,或是这些粒子的特定组合。
这个定义准确地表明:NA= 6.022 14076 ×1023mol-1,反向推导,依据确定常数NA即可给出摩尔的准确表达式:
这个定义的影响是一摩尔是个包含6.022 14076×1023个指定基本粒子的系统之物质的量。
以前的摩尔定义由碳12的摩尔质量M(12C)值确定,精确到0.012 kg/mol,然而现在M(12C)已经不再准确了,且必须用实验方法确定。在采用摩尔现在的定义的时候选择NA值,M(12C)等于0.012 kg/mol,其相对标准不确定度为4.5 ×10−10。
任何原子或分子的摩尔质量X可以从其相对原子质量的方程中得到:
M(X) = Ar(X) [M(12C)/12] = Ar(X) Mu
而任何一个原子或分子的摩尔质量X,也与基本粒子质量m(X)有关:
M(X) = NAm(X) = NAAr(X) mu
在这些方程中,Mu是摩尔质量常数,等于M(12C)/12,而mu是统一标准的原子量常数,等于m(12C)/12。它们由阿伏伽德罗常数通过下式关联:
Mu= NAmu
按照“物质的量”名称,在任何具体的应用中,“物质”这个词通常会被详细说明物质的词语所取代,以便可以唯一,例如:谈论“氯化氢的量,HCl”,或“苯的量,C6H6”,总是给出涉及实体的明确说明是非常重要的(正如摩尔定义中所强调的),这种给予涉及材料的化学分子式应该更好。尽管“量”这个词有更多综合的字典释义,但“物质的量(amount of substance)”全称缩写成“量(amount)”可用于简写。这也适用于导出量,比如“amount-of-substance concentration(物质的量浓度)”可简称为“amount concentration(量浓度)”。在临床生化领域名称“amount-of-substance concentration(物质的量浓度)”通常缩写成“substance concentration(物质浓度)”。
七 、坎德拉,(The candela),符号cd,是按一个指定方向的发光强度的SI单位
它由频率为540×1012Hz的单色辐射光光视效率的固定数值Kcd定义,其值是683,单位为lm W-1,等于cd sr W-1或cd sr kg-1m-2s3,其中千克、米和秒依据h、c和ΔνCs定义。
这个定义准确地表明:频率ν = 540 ×1012Hz的单色辐射光光视效率Kcd= 683 kg-1m-2s3 cd sr,反向推导,依据确定常数Kcd, h和ΔνCs即可给出坎德拉的准确表达式:
或者
这个定义的结果是1坎德拉是指在一个指定方向来源于频率为540×1012赫兹、辐射强度为1/683瓦特每球面度的单色辐射光的发光强度。